LESSON: Sampling Methods
| Site: | Mountain Heights Academy OER |
| Course: | Introductory Statistics Q1 |
| Book: | LESSON: Sampling Methods |
| Printed by: | Guest user |
| Date: | Sunday, 27 July 2025, 6:38 AM |
Survey Sampling Methods
In this video you will be introduced to what surveys are and how important the selection process is of who participates in surveys.
Non-Probability Samples

Voluntary Sample
In a voluntary sample, subjects "self-select" for participating in the survey. They may be interested in or feel strongly about the topic, they may want the perks/prizes for participating or have any other number of motivations for choosing to participate.

Television and radio stations often ask viewers/listeners to call in with opinions about a particular issue they are covering. The websites for these and other organizations also usually include some sort of online poll question of the day. Reality television shows and fan balloting in professional sports to choose all-star players make use of these types of polls as well. All of these polls usually come with a disclaimer stating that, “This is not a scientific poll.”
While perhaps entertaining, these types of polls are very susceptible to voluntary response bias. The people who respond to these types of surveys tend to feel very strongly one way or another about the issue in question, and the results might not reflect the overall population. Those who still have an opinion, but may not feel quite so passionately about the issue, may not be motivated to respond to the poll. This is especially true for phone-in or mail-in surveys in which there is a cost to participate. The effort or cost required tends to weed out much of the population in favor of those who hold extremely polarized views.
A news channel might show a report about a child killed in a drive-by shooting and then ask for people to call in and answer a question about tougher criminal sentencing laws. They would most likely receive responses from people who were very moved by the emotional nature of the story and wanted anything to be done to improve the situation.
An even bigger problem is present in those types of polls in which there is no control over how many times an individual may respond.

Convenience Sample
In a convenience sample, subjects are chosen because they are easy to reach because of their proximity to the researcher. These subjects are convenient to sample because they are close at hand.

Suppose your statistics teacher gave you an assignment to perform a survey of 20 individuals. You would most likely tend to ask your friends and family to participate, because it would be easy and quick. This is an example of convenience sampling, or convenience bias. While it is not always true, your friends are usually people who share common values, interests, and opinions. This could cause those opinions to be over-represented in relation to the true population.
Also, have you ever been approached by someone conducting a survey on the street or in a mall? If such a person were just to ask the first 20 people they found, there is the potential that large groups representing various opinions would not be included, resulting in undercoverage.

Probability Sample Methods

Simple Random Sample
When a Simple Random Sample of size

For example, if your statistics teacher wants to choose a student at random for a special prize, he or she could simply place the names of all the students in the class in a hat, mix them up, and choose one.
More scientifically, your teacher could assign each student in the class a number from 1 to 25 (assuming there are 25 students in the class) and then use a computer or calculator to generate a random number to choose one student. This would be a simple random sample of size 1.

Stratified Random Sample
When it's important for the sample to have members from different segments of the population to be surveyed, you should use a Stratified Random Sample.
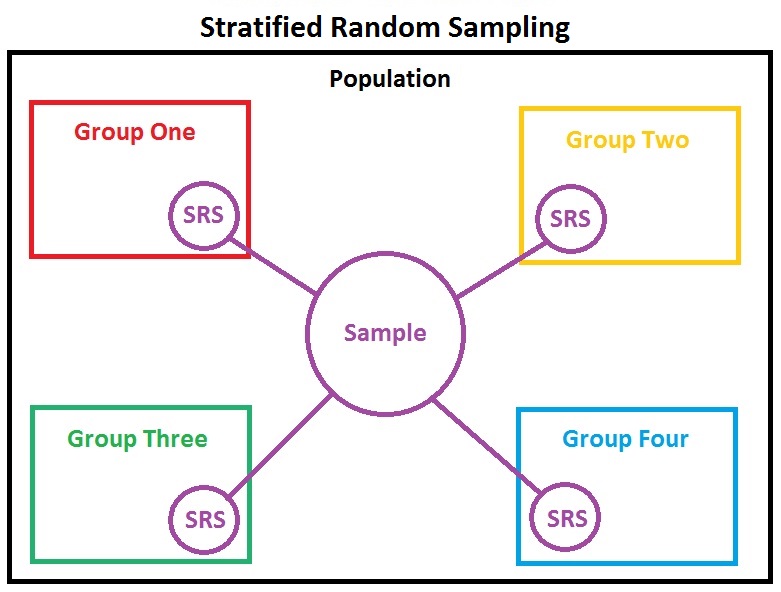
In a Stratified Random Sample the population is divided by some characteristic into groups called strata. For example, populations could be divided by gender, age, ethnicity, geographical location or even political preference. Then, a sample is then randomly selected (by simple random sample) from EACH strata. Using a Stratified Random Sample ensures that each segment of the population is represented.
Let's say an elementary school is going to conduct a survey to decide what foods students want included on the school lunch menu. Elementary schools span a large age group of kids with different likes and dislikes. To ensure that each grade level has an equal opportunity to voice their opinion on the topic the school uses a Stratified Random Sample. The school is divided into strata by grade level. Then, students are randomly selected (by SRS) from each grade level to participate in the lunch menu survey.
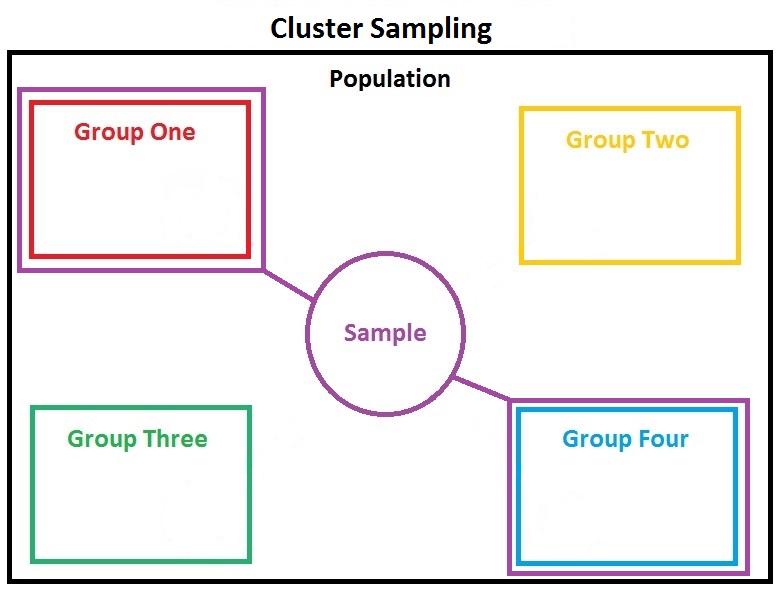
Cluster Sample
In Cluster Sampling, a population is divided into naturally occurring groups (or clusters). These types of groups generally have similar characteristics. For example, a population could be divided into clusters by county or zip codes. After the population is divided into clusters, some clusters are randomly selected. Then ALL subjects within those clusters are surveyed. Keep in mind, clusters are not like strata. Unlike strata, not all clusters are included in the sample.
Systematic Random Sample
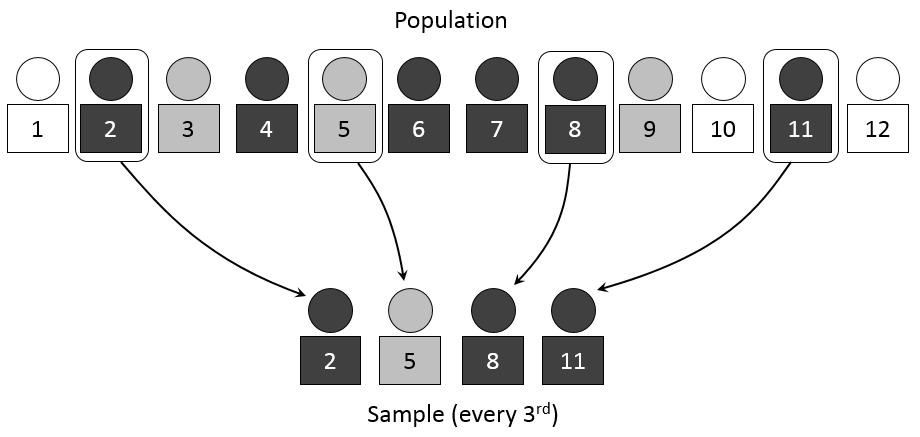
There are other types of samples that are not simple random samples, and one of these is a Systematic Random Sample. In systematic sampling, after choosing a starting point at random, subjects are selected using a jump number. If you have ever chosen teams or groups in gym class by counting off by threes or fours, you were engaged in systematic sampling.
The jump number is determined by dividing the population size by the desired sample size to insure that the sample combs through the entire population. If we had a list of everyone in your class of 12 students in alphabetical order, and we wanted to choose 4 of them, we would choose every 3rd student.
We would use a random number generator (on the computer or a calculator) to give us our starting point. Let's say our random number generator gave us the number 5.
In this case, we would start with student number 5 and then select every 3rd student until we had 4 in all. When we came to the end of the list, we would continue the count at number 1. Thus, our chosen students would be: 5, 8, 11, and 2. It is important to note that this is not a simple random sample, as not every possible sample of 4 students has an equal chance of being chosen. For example, it is impossible to have a sample consisting of students 5, 6, 7, and 8.

Multistage Sample
In Multistage Sampling, surveyors combine two or more sampling methods.
Let's go back to the example of the elementary school conducting a survey on what students want included on the school lunch menu.
Stage 1: Cluster Sampling - students are divided into clusters by grade level, some clusters are randomly selected to participate in the survey.
Stage 2: Systematic Random Sampling - instead of surveying all students in the selected clusters, we decide to pick a systematic random sampling by listing all members of each cluster on a paper and selecting every 10th student to participate in the survey.