LESSON: Extrapolation & Predicted Values
| Site: | Mountain Heights Academy OER |
| Course: | Introductory Statistics Q3 |
| Book: | LESSON: Extrapolation & Predicted Values |
| Printed by: | Guest user |
| Date: | Friday, 25 July 2025, 4:35 PM |
Extrapolation & Interpolation
When we use a regression line (linear or nonlinear) to make a prediction about are data set, there are two types of predictions that can be made:
Extrapolation
Extrapolated predictions are those that are made outside of the known data points. Trends in the known data can often be used to make accurate extrapolated predictions; however, this is not always the case. That's why it's best to avoid making extrapolated predictions. For example, a young man's parents kept track of his height through the years, as shown in the graph below. Extrapolation shows that Bryan will be about 10 feet tall when he's 30 years old. What faulty assumption was made in this extrapolation? 
Interpolation
Interpolated predictions are those that are made between known data points. An interpolation of this data would lead one to the prediction that Bryan was about 4.5 ft tall at the age of 14. Is this a reasonable prediction? Was your interpolated prediction more or less accurate than your extrapolated prediction? Typically, interpolated predictions are more accurate. Why do you think this is so? 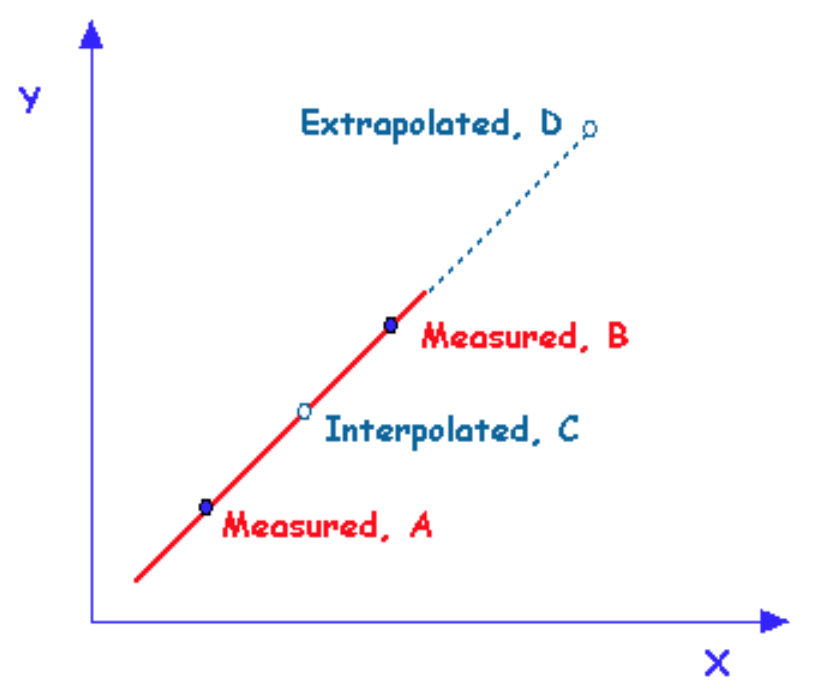
Malthusian Mistake
In 1798, a British economist published a study about world population. Thomas Robert Malthus’s conclusions horrified many people. He compared the growing population against the available resources. Based on his calculations, people were having too many children. He predicted that within a few generations, the world would run out of food. But more than 200 years later, the human race is still going strong. What happened to Malthus’s calculations?
Does the Past Predict the Future?
Malthus used extrapolation to predict how many people would exist in the future, and how much food they’d have. But past data can’t predict future inventions. When Malthus wrote his study, in 1798, farming required a lot of labor. Crops failed frequently, and it was difficult to ship food from one part of the world to another. If technology hadn’t evolved, Malthus’s dark predictions might have become reality. Malthus lived at the very beginning of the Industrial Revolution. He couldn’t begin to imagine the advancements that would later make it possible to feed billions of people with much less effort.
Today, we use machines to plant and harvest crops. We have genetically engineered drought- and blight-resistant seeds. Refrigeration, freeze-drying, and improved canning methods make it possible to ship food to anywhere in the world. In Malthus’s time, famines resulted from bad weather and bad luck. Today, most famines are a consequence of warfare or rule by oppressive dictators who deliberately deny their people food. Meanwhile, population growth has slowed, as countries have become wealthier. People now spend more money on education, wait to have children, and have fewer babies. Malthus’s predictions were good math but poor social science. He couldn’t foresee how technology would change many lives for the better.

Population Predictions
In almost all cases, extrapolation will lead to inaccurate predictions. It's impossible to know how inaccurate they are until they can be tested. Researchers and scientists know this and try to adjust their predictions based on the many different variables and logical reasoning available to them.
In this lesson video you will see how researchers in the UK are taking into account many different variables when trying to predict the future population of the world.
Residuals
Watch this lesson video to see how we can compare actual values to predicted values by looking at residuals. We will discuss how to do these calculations and graphs in the upcoming lesson videos.
Creating & Understanding Residual Plots
In the last lesson video you were introduced to the term "Residuals". Residuals calculate how far away the predicted values are from the actual value. In this lesson video you will learn how to create a residual plot by hand and then how to interpret the residual plot.
Looking at Real Data
Watch this video to see an example of what you will be asked to do on your upcoming assignment.

