Measures of Spread

Variance & Standard Deviation

The standard deviation is an extremely important measure of spread that is based on the mean. Recall that the mean (represented by $${\bar{x}}$$ and pronounced "x bar") is the numerical balancing point of the data. One way to measure how the data are spread is to look at how far away each of the values is from the mean. The difference between a data value and the mean is called the deviation. Written symbolically, it would be as follows:

$$Deviation = x - \bar{x}$$

Let’s take the simple data set of three randomly selected individuals’ shoe sizes shown below:

9.5   11.5   12

The mean of this data set is 11. The deviations are as follows:


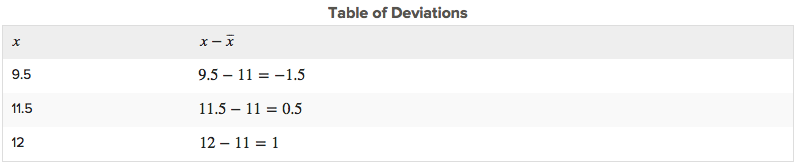
Notice that if a data value is less than the mean, the deviation of that value is negative. Data points that are greater than the mean have positive deviations.

The standard deviation is a measure of the typical, or average, deviation for all of the data points from the mean. However, the very property that makes the mean so special also makes it tricky to calculate a standard deviation. Because the mean is the balancing point of the data, when you add the deviations, they always sum to 0.


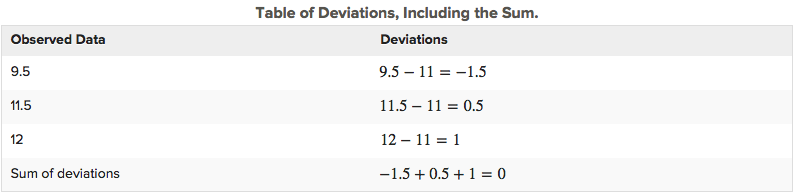
Therefore, we need all the deviations to be positive before we add them up. One way to do this that you might be thinking of would be to make them positive by taking their absolute values. This would work and it's a technique we use for a similar measure called the mean absolute deviation. For the standard deviation, though, we square all the deviations. The square of any real number is always positive.


We want to find the average of the squared deviations. To find an average, you usually divide by the number of data points in your set, n. If we were finding the standard deviation for an entire population then we would divide by n. However, in this example, we are only working with a sample of a population, so we will divide by n - 1. Since n = 3, you will divide 3.5 by 2.

The result, which is called the variance, is $$3.5/2=1.75$$. The variance of a sample is denoted by $$s^{2}$$ or the Greek letter $$\sigma^{2}$$ and is a measure of how closely the data are clustered around the mean. Because we squared the deviations before we added them, the units we were working in were also squared. 

To return to the original units, we must take the square root of our result: $$\sqrt{1.75}=1.32$$. 

This quantity is the standard deviation and is denoted by s or the Greek letter sigma $$\sigma$$. The number indicates that in our sample, the typical data value is approximately 1.32 units away from the mean. It is a measure of how closely the data are clustered around the mean. 

A small standard deviation means that the data points are clustered close to the mean, while a large standard deviation means that the data points are spread out from the mean.