Introduction to Confidence Intervals


Confidence Intervals

The general concept of confidence intervals is pretty intuitive: It is easier to predict that an unknown value will lie somewhere within a wide range, than to predict it will occur within a narrow range. In other words, if you are making an educated guess about an unknown number, you are more likely to be correct if you predict it will occur within a wider range. This idea is reflected in the concept question above, where the reward is greater if you guess within a smaller range, because the contest creator knows that your chance of guessing correctly is much less if you have to guess within a smaller range. 

A confidence interval, centered on the mean of your sample, is the range of values that is expected to capture the population mean with a given level of confidence. A wider confidence interval is a greater range of values, resulting in a greater confidence level that the range will include the population mean. By convention, you will mostly be concerned with identifying the intervals associated with 90%, 95%, and 99% confidence levels.

Calculate the confidence interval by combining the sample mean with the margin of error, found by multiplying the standard error of the mean by the z-score of the percent confidence level:


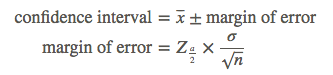
It is common, but incorrect, to assume that a confidence level indicates the probability that the mean of the population will occur within a given range of the mean of your sample. A 95% confidence interval means that if you took 100 samples, all of the same size, and formed 100 confidence intervals, 95 of these intervals would capture the population mean.

The confidence level indicates the number of times out of 100 that the mean of the population will be within the given interval of the sample mean.